Extrema Theresaleeann The first derivative proves the function's increase decrease (if the first derivative is positive, the function is increasing and vice versa). you're right on the test though. the first derivative test is indeed used to prove the existence of critical points. the second derivative itself doesn't prove concavity. To determine if a critical point is a relative extrema (and in fact to determine if it is a minimum or a maximum) we can use the following fact. fact suppose that \(\left( {a,b} \right)\) is a critical point of \(f\left( {x,y} \right)\) and that the second order partial derivatives are continuous in some region that contains \(\left( {a,b} \right)\).
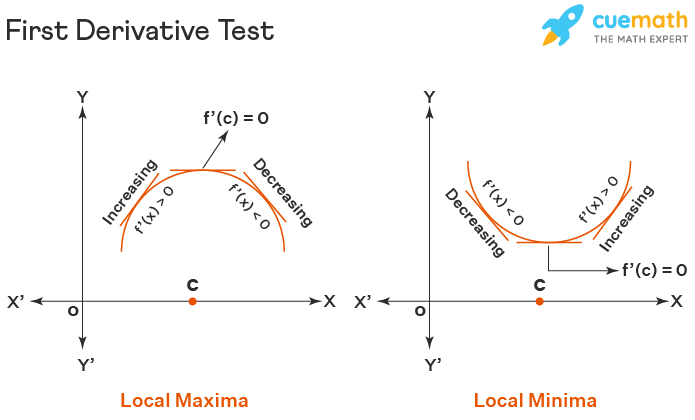
Quantuminous Rhythmical Can Jobs Top Used Enterprise Size Businesses This calculus video tutorial explains how to find the relative extrema of a function such as the local maximum and minimum values using the first derivative. Try graphing the function y = x^3 2x^2 .2x. you have a local maximum and minimum in the interval x = 1 to x = about .25. by looking at the graph you can see that the change in slope to the left of the maximum is steeper than to the right of the maximum. Fact 31.1 the first derivative test (for finding local extrema.) suppose c is a critical point of f(x). 1. if f0(x) changes from to ° at c, then f(x) has a local maximum at c. 2. if f0(x) changes from ° to at c, then f(x) has a local minimum at . 3. if f0(x) does not change sign at c, there is no local extremum at c. the graph below. Use the first derivative test to find the location of all local extrema for f(x) = x3 − 3x2 − 9x − 1. use a graphing utility to confirm your results. solution. step 1. the derivative is f ′ (x) = 3x2 − 6x − 9. to find the critical points, we need to find where f ′ (x) = 0.
Konsep Terkini 20 Max Formula 1 Fact 31.1 the first derivative test (for finding local extrema.) suppose c is a critical point of f(x). 1. if f0(x) changes from to ° at c, then f(x) has a local maximum at c. 2. if f0(x) changes from ° to at c, then f(x) has a local minimum at . 3. if f0(x) does not change sign at c, there is no local extremum at c. the graph below. Use the first derivative test to find the location of all local extrema for f(x) = x3 − 3x2 − 9x − 1. use a graphing utility to confirm your results. solution. step 1. the derivative is f ′ (x) = 3x2 − 6x − 9. to find the critical points, we need to find where f ′ (x) = 0. Example 2: evaluate the relative extrema of the function f (x) = x 3 6x 2 9x 15. solution: we will use the second derivative test to find the relative extrema of the function f (x) = x 3 6x 2 9x 15. we will find the first derivative of f (x) to determine the critical points. f' (x) = 3x 2 12x 9. Use the first derivative test and the results of step 2 to determine whether [latex]f[ latex] has a local maximum, a local minimum, or neither at each of the critical points. recall from chapter 4.3 that when talking about local extrema, the value of the extremum is the y value and the location of the extremum is the x value.
First Derivative Test Examples Steps Applications Example 2: evaluate the relative extrema of the function f (x) = x 3 6x 2 9x 15. solution: we will use the second derivative test to find the relative extrema of the function f (x) = x 3 6x 2 9x 15. we will find the first derivative of f (x) to determine the critical points. f' (x) = 3x 2 12x 9. Use the first derivative test and the results of step 2 to determine whether [latex]f[ latex] has a local maximum, a local minimum, or neither at each of the critical points. recall from chapter 4.3 that when talking about local extrema, the value of the extremum is the y value and the location of the extremum is the x value.
Comments are closed.